Write an Arc Function With Processing Turtle Library

Blocks based Logo environments that have an arc block, such as TurtleArt, allow you to input the angle of the arc you want to draw, as well as the radius of the circle it is on.

There isn't an arc function in Leah Beuchley's Processing Turtle library. A great challenge is to write your own arc function, and I think high school students would have a great time with this, too. I'm going to break down this problem step by step.

The Turtle, with its self awareness of its own heading and ability to move a given distance between two points, makes it possible to think of a circle as 360 iterations of a step forward and a turn of one degree. The Turtle class is doing the trigonometry behind the scenes that converts its rotation from the Cartesian plane to Turtle Geometry.

 for (int i = 0; i<360; i++) {  
   t.forward(1);  
   t.right(1);  
  }  

This can be made into its own function by wrapping it in its own void type function definition:

 void circle() {  
  for (int i = 0; i<360; i++) {  
   t.forward(1);  
   t.right(1);  
  }  
 }  

Of course you would want to make the function adaptable to different size inputs, so let's add a radius parameter. To do that you have to dig into the relationship between a circle's radius and its circumference: C=2πr. If we pass in a radius value, we can define a circumference value as a result of this equation: void circle(int radius) {
  float c = TWO_PI*radius;
Now the distance the turtle steps forward each of the 360 times will be equal to c/360. To put it all together so far:

 import Turtle.*;  
 Turtle t;  
 void setup() {  
  size(500, 500);  
  t = new Turtle(this);  
  background(255);  
  noLoop();  
 }   
 void draw() {  
  circle(50);  
  circle(100);  
 }  
 void circle(int radius) {  
  float c = TWO_PI*radius;  
  for (int i = 0; i<360; i++) {  
   t.forward(c/360);  
   t.right(1);  
  }  
 }  

The next step is to draw only part of the circle, an arc. That is simpler than I had at first thought! We can just add an angle parameter, which is used to set the number of times to iterate the for loop:

 void arc(int angle, int radius) {  
  ...  
  for (int i = 0; i<angle; i++) {  

Putting this all together:

 import Turtle.*;  
 Turtle t;  
 void setup() {  
  size(500, 500);  
  t = new Turtle(this);  
  background(255);  
  noLoop();  
 }   
 void draw() {  
  arc(90,50);  
 }  
 void arc(int angle, int radius) {  
  float c = TWO_PI*radius;  
  for (int i = 0; i<angle; i++) {  
   t.forward(c/360);  
   t.right(1);  
  }  
 }  

At this point you can make any size arc with any radius, but it can only go to the right. To make an arc go to the left, TurtleArt has you put in a negative angle amount:

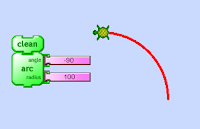
This is an interesting problem to solve! Here's the pseudo-code, as I think of it:
Inside the iteration part of the arc function:
If the value of angle is greater than zero, turn right 1
else turn left 1
And since we're also using the angle value to set the number of iterations of the for loop, that needs to be an absolute value: for (int i = 0; i<abs(angle); i++) {
So the function ends up looking like this:

 void arc(int angle, int radius) {  
  float c = TWO_PI*radius;  
  for (int i = 0; i<abs(angle); i++) {  
   t.forward(c/360);  
   if (angle > 0) {  
    t.right(1);  
   } else {  
    t.left(1);  
   }  
  }  
 }  

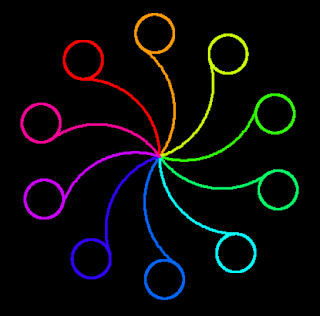
Now it's time to have fun with it!

 import Turtle.*;  
 Turtle t;  
 void setup() {  
  size(500, 500);  
  t = new Turtle(this);  
  background(0);  
  colorMode(HSB, 100, 100, 100);  
  strokeWeight(3);  
  noLoop();  
 }   
 void draw() {  
  for (int i = 0; i<10; i++) {  
   stroke(i*10, 100, 100);  
   t.setHeading(i*36);  
   arc(-90, 100);  
   arc(360, 25);  
   t.goToPoint(width/2, height/2);  
  }  
 }  
 void arc(int angle, int radius) {  
  float c = TWO_PI*radius;  
  for (int i = 0; i<abs(angle); i++) {  
   t.forward(c/360);  
   if (angle > 0) {  
    t.right(1);  
   } else {  
    t.left(1);  
   }  
  }  
 }